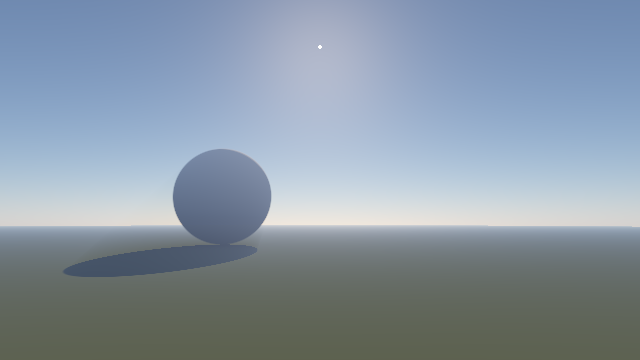
This GLSL file is used to render the test scene in model_test.cc, on GPU and CPU, in order to evaluate the approximations made in the GPU atmosphere model. For this reason, as for the GPU model shaders, it is written in such a way that it can be compiled either with a GLSL compiler, or with a C++ compiler.

The test scene, shown above, is a sphere S on a purely spherical planet P. It is rendered by "ray tracing", i.e. the vertex shader outputs the view ray direction, and the fragment shader computes the intersection of this ray with the spheres S and P to produce the final pixels. The fragment shader also computes the intersection of the light rays with the sphere S, to compute shadows, as well as the intersections of the view ray with the shadow volume of S, in order to compute light shafts.
The functions to compute shadows and light shafts must be defined before we can use them in the main shader function, so we define them first. Testing if a point is in the shadow of the sphere S is equivalent to test if the corresponding light ray intersects the sphere, which is very simple to do. However, this is only valid for a punctual light source, which is not the case of the Sun. In the following function we compute an approximate (and biased) soft shadow by taking the angular size of the Sun into account:
Number GetSunVisibility(Position point, Direction sun_direction) {
Position p = point - kSphereCenter;
Length p_dot_v = dot(p, sun_direction);
Area p_dot_p = dot(p, p);
Area ray_sphere_center_squared_distance = p_dot_p - p_dot_v * p_dot_v;
Length distance_to_intersection = -p_dot_v - sqrt(
kSphereRadius * kSphereRadius - ray_sphere_center_squared_distance);
if (distance_to_intersection > 0.0 * m) {
// Compute the distance between the view ray and the sphere, and the
// corresponding (tangent of the) subtended angle. Finally, use this to
// compute an approximate sun visibility.
Length ray_sphere_distance =
kSphereRadius - sqrt(ray_sphere_center_squared_distance);
Number ray_sphere_angular_distance = -ray_sphere_distance / p_dot_v;
return smoothstep(
Number(1.0), Number(0.0), ray_sphere_angular_distance / sun_size_.x);
}
return 1.0;
}
The sphere also partially occludes the sky light, and we approximate this effect with an ambient occlusion factor. The ambient occlusion factor due to a sphere is given in Radiation View Factors (Isidoro Martinez, 1995). In the simple case where the sphere is fully visible, it is given by the following function:
Number GetSkyVisibility(Position point) {
Position p = point - kSphereCenter;
Area p_dot_p = dot(p, p);
return
1.0 + p.z / sqrt(p_dot_p) * kSphereRadius * kSphereRadius / p_dot_p;
}
To compute light shafts we need the intersections of the view ray with the shadow volume of the sphere S. Since the Sun is not a punctual light source this shadow volume is not a cylinder but a cone (for the umbra, plus another cone for the penumbra, but we ignore it here):
Noting, as in the above figure, $\bp$ the camera position, $\bv$ and $\bs$ the unit view ray and sun direction vectors and $R$ the sphere radius (supposed to be centered on the origin), the point at distance $d$ from the camera is $\bq=\bp+d\bv$. This point is at a distance $\delta=-\bq\cdot\bs$ from the sphere center along the umbra cone axis, and at a distance $r$ from this axis given by $r^2=\bq\cdot\bq-\delta^2$. Finally, at distance $\delta$ along the axis the umbra cone has radius $\rho=R-\delta\tan\alpha$, where $\alpha$ is the Sun's angular radius. The point at distance $d$ from the camera is on the shadow cone only if $r^2=\rho^2$, i.e. only if \begin{equation} (\bp+d\bv)\cdot(\bp+d\bv)-((\bp+d\bv)\cdot\bs)^2= (R+((\bp+d\bv)\cdot\bs)\tan\alpha)^2 \end{equation} Developping this gives a quadratic equation for $d$: \begin{equation} ad^2+2bd+c=0 \end{equation} where
void GetSphereShadowInOut(Direction view_direction, Direction sun_direction,
OUT(Length) d_in, OUT(Length) d_out) {
Position pos = camera_ - kSphereCenter;
Length pos_dot_sun = dot(pos, sun_direction_);
Number view_dot_sun = dot(view_direction, sun_direction_);
Number k = sun_size_.x;
Number l = 1.0 + k * k;
Number a = 1.0 - l * view_dot_sun * view_dot_sun;
Length b = dot(pos, view_direction) - l * pos_dot_sun * view_dot_sun -
k * kSphereRadius * view_dot_sun;
Area c = dot(pos, pos) - l * pos_dot_sun * pos_dot_sun -
2.0 * k * kSphereRadius * pos_dot_sun - kSphereRadius * kSphereRadius;
Area discriminant = b * b - a * c;
if (discriminant > 0.0 * m2) {
d_in = max(0.0 * m, (-b - sqrt(discriminant)) / a);
d_out = (-b + sqrt(discriminant)) / a;
// The values of d for which delta is equal to 0 and kSphereRadius / k.
Length d_base = -pos_dot_sun / view_dot_sun;
Length d_apex = -(pos_dot_sun + kSphereRadius / k) / view_dot_sun;
if (view_dot_sun > 0.0) {
d_in = max(d_in, d_apex);
d_out = a > 0.0 ? min(d_out, d_base) : d_base;
} else {
d_in = a > 0.0 ? max(d_in, d_base) : d_base;
d_out = min(d_out, d_apex);
}
} else {
d_in = 0.0 * m;
d_out = 0.0 * m;
}
}
Using these functions we can now implement the main shader function, which computes the radiance from the scene for a given view ray. This function first tests if the view ray intersects the sphere S. If so it computes the sun and sky light received by the sphere at the intersection point, combines this with the sphere BRDF and the aerial perspective between the camera and the sphere. It then does the same with the ground, i.e. with the planet sphere P, and then computes the sky radiance and transmittance. Finally, all these terms are composited together (an opacity is also computed for each object, using an approximate view cone - sphere intersection factor) to get the final radiance.
We start with the computation of the intersections of the view ray with the shadow volume of the sphere, because they are needed to get the aerial perspective for the sphere and the planet:
RadianceSpectrum GetViewRayRadiance(Direction view_ray,
Direction view_ray_diff) {
// Normalized view direction vector.
Direction view_direction = normalize(view_ray);
// Tangent of the angle subtended by this fragment.
Number fragment_angular_size = length(view_ray_diff) / length(view_ray);
Length shadow_in;
Length shadow_out;
GetSphereShadowInOut(view_direction, sun_direction_, shadow_in, shadow_out);
We then test whether the view ray intersects the sphere S or not. If it does,
we compute an approximate (and biased) opacity value, using the same
approximation as in GetSunVisibility:
// Compute the distance between the view ray line and the sphere center,
// and the distance between the camera and the intersection of the view
// ray with the sphere (or NaN if there is no intersection).
Position p = camera_ - kSphereCenter;
Length p_dot_v = dot(p, view_direction);
Area p_dot_p = dot(p, p);
Area ray_sphere_center_squared_distance = p_dot_p - p_dot_v * p_dot_v;
Length distance_to_intersection = -p_dot_v - sqrt(
kSphereRadius * kSphereRadius - ray_sphere_center_squared_distance);
// Compute the radiance reflected by the sphere, if the ray intersects it.
Number sphere_alpha = 0.0;
RadianceSpectrum sphere_radiance =
RadianceSpectrum(0.0 * watt_per_square_meter_per_sr_per_nm);
if (distance_to_intersection > 0.0 * m) {
// Compute the distance between the view ray and the sphere, and the
// corresponding (tangent of the) subtended angle. Finally, use this to
// compute the approximate analytic antialiasing factor sphere_alpha.
Length ray_sphere_distance =
kSphereRadius - sqrt(ray_sphere_center_squared_distance);
Number ray_sphere_angular_distance = -ray_sphere_distance / p_dot_v;
sphere_alpha =
min(ray_sphere_angular_distance / fragment_angular_size, 1.0);
We can then compute the intersection point and its normal, and use them to get the sun and sky irradiance received at this point. The reflected radiance follows, by multiplying the irradiance with the sphere BRDF:
Position point = camera_ + view_direction * distance_to_intersection;
Direction normal = normalize(point - kSphereCenter);
// Compute the radiance reflected by the sphere.
IrradianceSpectrum sky_irradiance;
IrradianceSpectrum sun_irradiance = GetSunAndSkyIrradiance(
point - earth_center_, normal, sun_direction_, sky_irradiance);
sphere_radiance =
sphere_albedo_ * (1.0 / (PI * sr)) * (sun_irradiance + sky_irradiance);
Finally, we take into account the aerial perspective between the camera and the sphere, which depends on the length of this segment which is in shadow:
Length shadow_length =
max(0.0 * m, min(shadow_out, distance_to_intersection) - shadow_in);
DimensionlessSpectrum transmittance;
RadianceSpectrum in_scatter = GetSkyRadianceToPoint(camera_ - earth_center_,
point - earth_center_, shadow_length, sun_direction_, transmittance);
sphere_radiance = sphere_radiance * transmittance + in_scatter;
}
In the following we repeat the same steps as above, but for the planet sphere P instead of the sphere S (a smooth opacity is not really needed here, so we don't compute it. Note also how we modulate the sun and sky irradiance received on the ground by the sun and sky visibility factors):
// Compute the distance between the view ray line and the Earth center,
// and the distance between the camera and the intersection of the view
// ray with the ground (or NaN if there is no intersection).
p = camera_ - earth_center_;
p_dot_v = dot(p, view_direction);
p_dot_p = dot(p, p);
Area ray_earth_center_squared_distance = p_dot_p - p_dot_v * p_dot_v;
distance_to_intersection = -p_dot_v - sqrt(
earth_center_.z * earth_center_.z - ray_earth_center_squared_distance);
// Compute the radiance reflected by the ground, if the ray intersects it.
Number ground_alpha = 0.0;
RadianceSpectrum ground_radiance =
RadianceSpectrum(0.0 * watt_per_square_meter_per_sr_per_nm);
if (distance_to_intersection > 0.0 * m) {
Position point = camera_ + view_direction * distance_to_intersection;
Direction normal = normalize(point - earth_center_);
// Compute the radiance reflected by the ground.
IrradianceSpectrum sky_irradiance;
IrradianceSpectrum sun_irradiance = GetSunAndSkyIrradiance(
point - earth_center_, normal, sun_direction_, sky_irradiance);
ground_radiance = ground_albedo_ * (1.0 / (PI * sr)) * (
sun_irradiance * GetSunVisibility(point, sun_direction_) +
sky_irradiance * GetSkyVisibility(point));
Length shadow_length =
max(0.0 * m, min(shadow_out, distance_to_intersection) - shadow_in);
DimensionlessSpectrum transmittance;
RadianceSpectrum in_scatter = GetSkyRadianceToPoint(camera_ - earth_center_,
point - earth_center_, shadow_length, sun_direction_, transmittance);
ground_radiance = ground_radiance * transmittance + in_scatter;
ground_alpha = 1.0;
}
Finally, we compute the radiance and transmittance of the sky, and composite together, from back to front, the radiance and opacities of all the ojects of the scene:
// Compute the radiance of the sky.
Length shadow_length = max(0.0 * m, shadow_out - shadow_in);
DimensionlessSpectrum transmittance;
RadianceSpectrum radiance = GetSkyRadiance(
camera_ - earth_center_, view_direction, shadow_length, sun_direction_,
transmittance);
// If the view ray intersects the Sun, add the Sun radiance.
if (dot(view_direction, sun_direction_) > sun_size_.y) {
radiance = radiance + transmittance * GetSolarRadiance();
}
radiance = radiance * (1.0 - ground_alpha) + ground_radiance * ground_alpha;
radiance = radiance * (1.0 - sphere_alpha) + sphere_radiance * sphere_alpha;
return radiance;
}